Record du monde sur 800m, JO Londres 2012
(D.Rudisha): mesures de vitesse moyenne tous les 100m (carrés rouges)
en m/sec comparées au calcul moyenné tous les 100m (étoiles bleues).
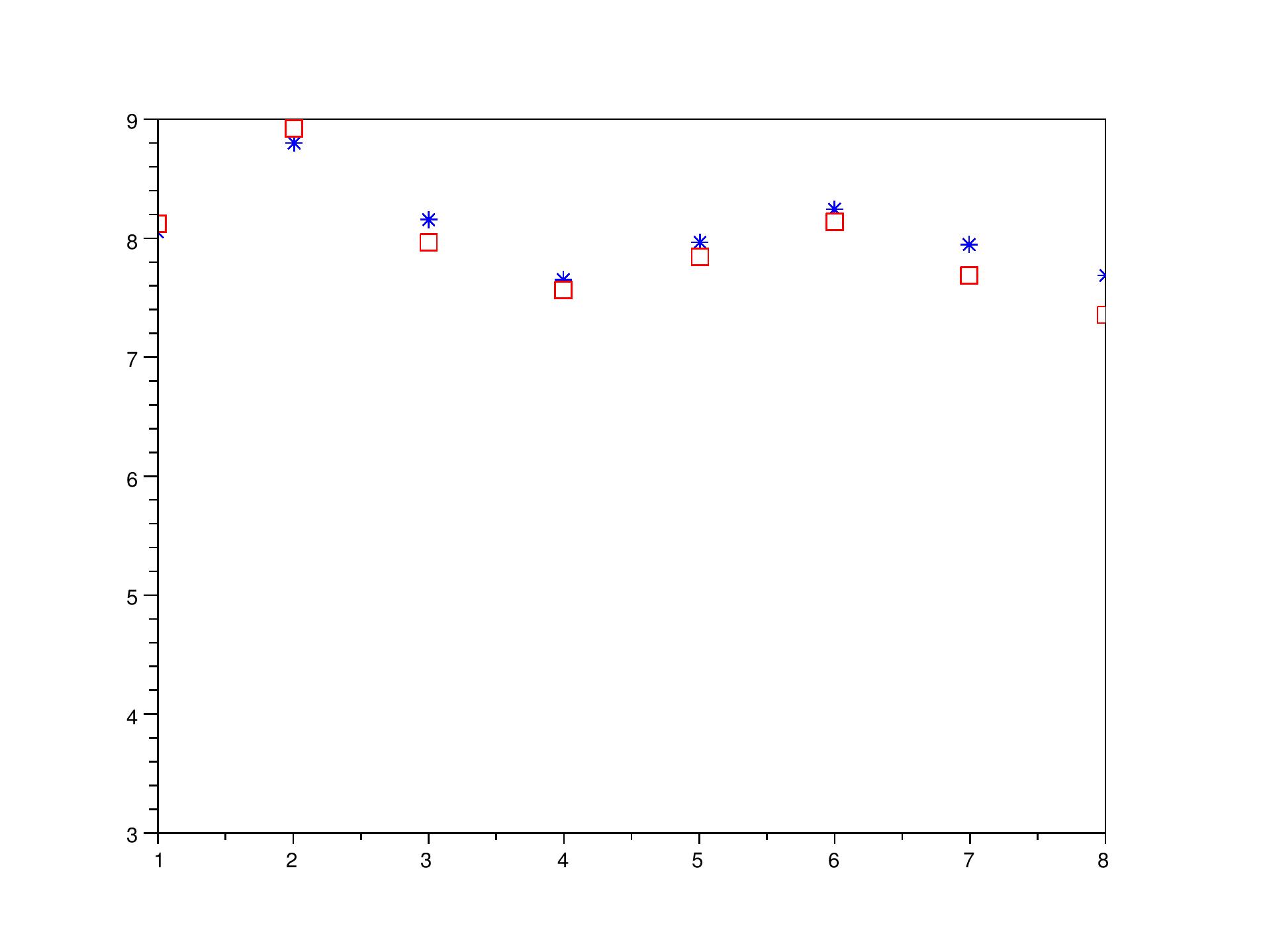
* le negative split: il vaut mieux courir la 2ème partie de
la course plus vite que la première
*il faut varier sa vitesse, ce qui permet de gagner par exemple 0.7% sur 800m.
En effet, quand on ralentit, on recrée un peu d'énergie, ce qui permet
d'améliorer son temps de course.
Sur les marathons par exemple, les coureurs sont invités à choisir une couleur en fonction de leur temps de course espéré (2h30, 3h, 4h, 5h etc). Cette couleur est associée à un ballon ou lièvre qui va se déplacer à vitesse constante pour arriver à la fin de la course dans le temps escompté. Et pourtant, tout coureur qui a couru un marathon s’est rendu compte qu’il avait envie de varier sa vitesse, en accélérant puis ralentissant. Oui, c’est normal, c’est ainsi que l’organisme arrive à régénérer un peu d’énergie.
Comment arriver à calculer à chaque instant la vitesse et
l'énergie disponibles pour un coureur? Cela nécessite un système d’équations différentielles, c’est-à-dire des
équations reliant la vitesse (et sa dérivée l’accélération), la force de
propulsion, les forces de frottement et l’énergie. Les équations reposent sur
le principe fondamental de la dynamique et des bilans d’énergie faisant
intervenir notamment VO2max, la consommation maximale d’oxygène du coureur, et
les liens de contrôle entre ces variables : par exemple, la recréation d’énergie
quand on ralentit. Pour être bien posé, le système est couplé à des conditions
initiales (vitesse nulle et énergie donnée au départ) et des contraintes :
l’énergie doit rester positive, la force de propulsion aussi (on ne recule pas !)
et cette force est bornée par les capacités limitées du coureur ; enfin la
dérivée de cette force de propulsion est bornée aussi car les informations ont
besoin de temps pour passer du cerveau à la jambe : le coureur ne peut pas
instantanément comme un ordinateur, passer d’une force de propulsion maximum à
l’arrêt complet. Le travail de modélisation consiste à bien poser ce système.
Mathématiquement, nous arrivons à prouver des théorèmes sur le comportement des
solutions.
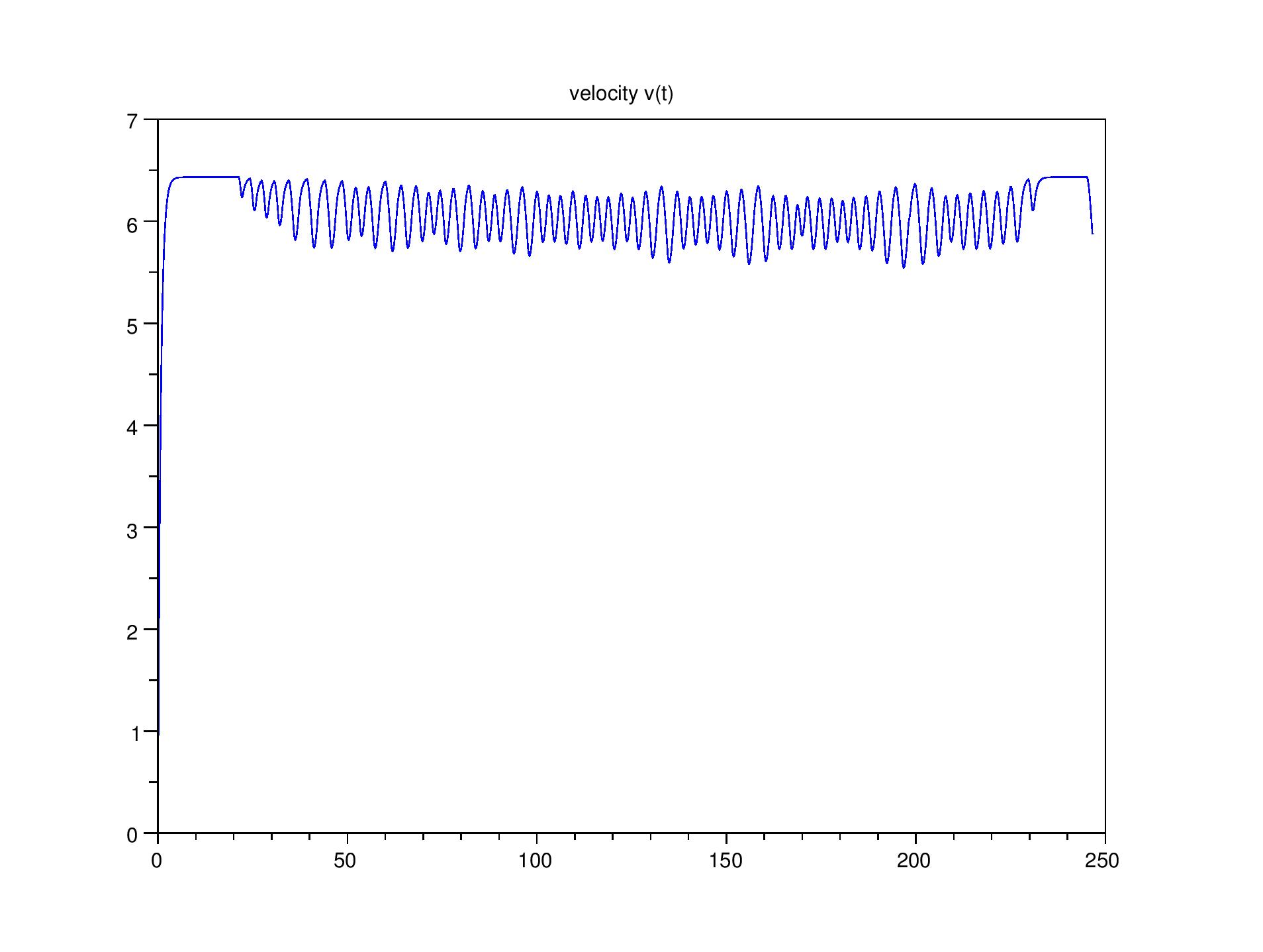
En particulier, quand on rajoute un terme de recréation d'énergie due
au ralentissement, on se rend compte que cela crée des termes concaves
dans le hamiltonien qui sont à l'origine des oscillations de vitesse.
Enfin, numériquement, nous sommes
capables de résoudre ce système d’équations pour calculer les valeurs
de toutes
les variables intéressantes pour le coureur et les relier aux mesures
physiologiques. Nos simulations numériques nécessitent une
programmation complexe et jamais réalisées sur ce type d'exemples.
Elles utilisent le logiciel Bocop,
qui nous a permis de résoudre le système d'équations différentielles
couplées, sous contraintes, et avec contrôle optimal.
A quoi cela
pourrait-il servir ? On se pose souvent la question de : à quoi
servent les mathématiques? Les
applications en sont pourtant immenses. Dans le cas de la course à pied,
on pourrait, à partir des équations que nous avons établies, imaginer un
logiciel qui calcule sur un smart-phone
*la vitesse optimale de course et donne des indications au coureur sur des
bases scientifiques
* la dépense énergétique et permet de voir comment elle aurait pu être
meilleure. On peut alors savoir exactement le nombre de calories perdues lors
d'une course, et pas avec une estimation moyenne comme le font tous les calculs
actuels, mais véritablement avec un calcul exact instantané.
 |
 |
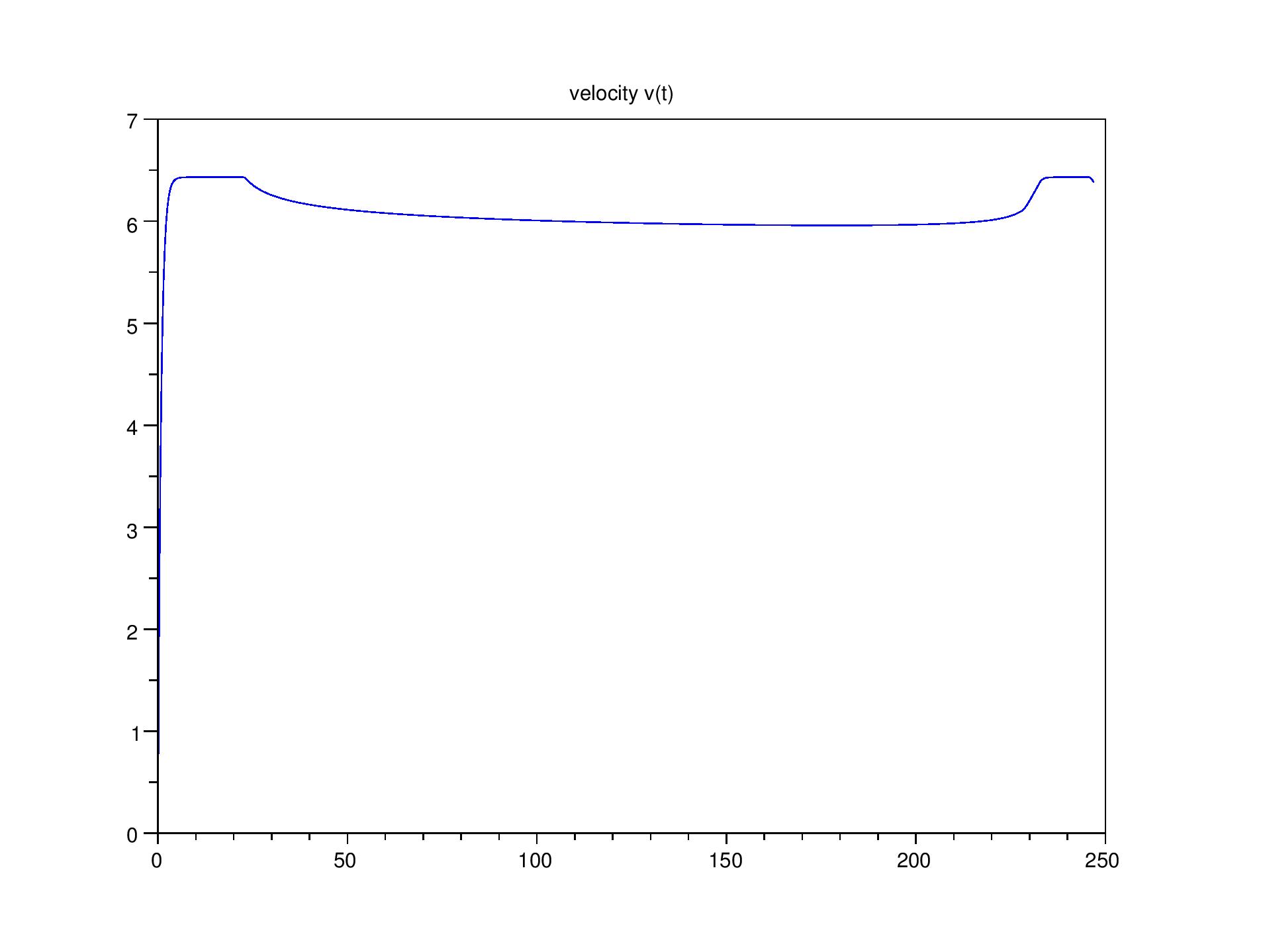
A gauche : sur un 1500m, profil de vitesse sans prendre
en compte la recréation d'énergie quand on
ralentit (on tient juste compte de la chute du VO2max en fin de course quand la
réserve d’énergie anaérobie est trop faible)
A droite : quand on prend en compte la recréation d’énergie en ralentissant, la vitesse oscille.
|
|